kwpolt.blogg.se - Differential calculus product rule

#Differential calculus product rule free#

Because such pebbles were used for counting out distances, tallying votes, and doing abacus arithmetic, the word came to mean a method of computation. The word calculus is Latin for "small pebble" (the diminutive of calx, meaning "stone"), a meaning which still persists in medicine. In mathematics education, calculus denotes courses of elementary mathematical analysis, which are mainly devoted to the study of functions and limits.

#Differential calculus product rule free#

So, product rule is used when two different functions are given. One function is not dependent on the other function.įrom above discussion we can conclude that we should use chain rule when you see functions to be differentiated within each other and use the product rule when you see functions to be differentiated in multiplication that is when the two functions are in product form.Look up calculus in Wiktionary, the free dictionary.

‘ \displaystyle ).īut one thing to be kept in mind here is that they both are separate functions one do not rely on the answer to the other.

In this case we will use the product rule because here we have two separate functions multiplied together. To the contrary, if the given function is of the form say, So, we use chain rule to differentiate these types of functions that means composite functions where one function contains another function. #Function two takes the sine of the answer given by the function one. # Function one takes x and multiplies it by 3. The two functions in the above example are as follows: It is generally a function that is written inside another function. Suppose we are given two functions, with the help of these two functions we can create another function by composing one function into the other. This is an example of a composite function means a “function of a function” or “function within a function”.Ī function that depends on any other function is called a composite function. Here in this case there are two functions not function of a function. Let us clear the difference between these two methods with the help of example: We use the product rule in differentiation when two functions are multiplied together such as f ( x ) * g ( x ) in general. We use the chain rule when differentiating a composite function that is a “function of a function”, like f in general. These are two really useful rules for differentiating functions. Now the question is how we will come to know whether we have to use chain rule or product rule to find the derivative of the given function.

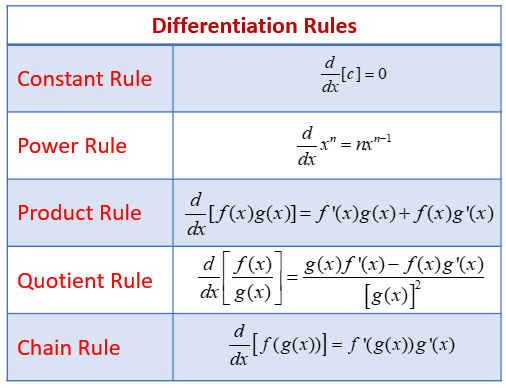
It is read as the derivative of function ‘f’ with respect to the variable x. There are different methods to find the derivatives of the given functions. These methods are: We can explain it as the measure of the rate at which the value of y changes with respect to the change of the variable x. The derivative of a constant function is always zero. But, to differentiate a function the rules of derivatives must be known. calculating the derivative requires the use of basic definition very rarely. Differentiation is one of the two key areas of calculus apart from Integration.ĭifferentiation i.e. Differentiation in mathematics is the rate of change of a function with respect to a variable.